Definition
An AVL tree is a binary search tree that is self-balancing based on the height of the tree. It manages this by adding a balance factor property to each node. Given a node \(X\), the balance factor is defined as:
\[ \text{BF}(X) = \text{Height}(\text{Left}(X)) - \text{Height}(\text{Right}(X)) \]
An binary tree is \textbf{left-heavy} when \(\text{BF}(X) < 0\) and \textbf{right-heavy} when \(\text{BF}(X) > 0\). An AVL tree is a binary search tree that is balanced if for every node \(X\), \(|\text{BF}(X)| \leq 1\).
Operations
Search and Traversal
Searching in an AVL tree is the same as searching with Binary Search Trees.
Insertion
Insertion largely follows the same process as with binary search trees. The key difference is based on the requirement to maintain the balance property. After inserting a new node, the balance factor of each node in the path from the root to the new node must be checked. If the balance factor of any node is greater than 1 or less than -1, the tree must be rebalanced.
Deletion
After a node is removed in the style of binary search trees, rebalancing may be necessary. At the very least, the balance factor of each node in the path from the root to the removed node must be updated.
Rebalancing
If a node is added to a perfectly balanced AVL tree, where \(BF(X) = 0\) for all nodes \(X\), the tree will remain balanced. Rebalancing then is only necessary when a node is added to a tree with a balance factor of 1 or -1. There are four possible cases for rebalancing an AVL tree based on the balance factor of \(X\):
- Left-Left (LL) - \(X\) is left-heavy and its left child is higher than its right child.
- Right-Right (RR) - \(X\) is right-heavy and its right child is higher than its left child.
- Left-Right (LR) - \(X\) is left-heavy and its right child is higher than its left child.
- Right-Left (RL) - \(X\) is right-heavy and its left child is higher than its right child.
Left-Left and Right-Right
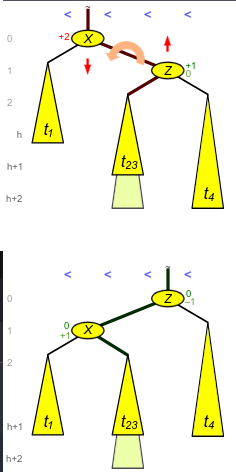
Consider a new node added to an AVL tree that causes an RR violation. This is shown in the figure below. The top half shows the tree during the violation. This was caused by either deleting a node from \(t_1\) or adding a node to \(t_4\). In this case a left rotation is performed to correct the violation.
There is still the matter of updating the balance factors of the \(X\) and \(Z\). If \(t_{23}\) was previously shorter than \(t_4\), the balance factor of \(X\) and \(Z\) after the rotation will be 0. If \(t_{23}\) was the same height as \(t_4\), the balance factor of \(X\) will be +1 and \(Z\) will be -1.
Figure 1: An AVL tree with a right-right violation (Wikipedia).
The case will be reversed for a left-left violation, where a right rotation is performed.
Left-Right and Right-Left
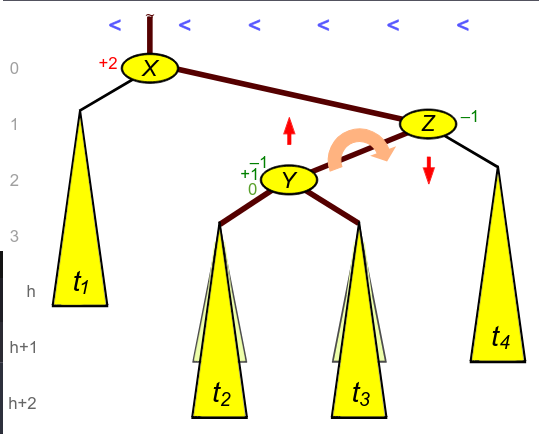
The figure below shows a tree with a Right-Left violation. This can happen if either a node was removed from \(t_1\) or a node was added to \(Y\), in which case the heights of \(t_2\) and \(t_3\) are not equal. Either way, the right side of the tree needs to be restructured to correct the violation.
Figure 2: An AVL tree with a right-left violation (Wikipedia).
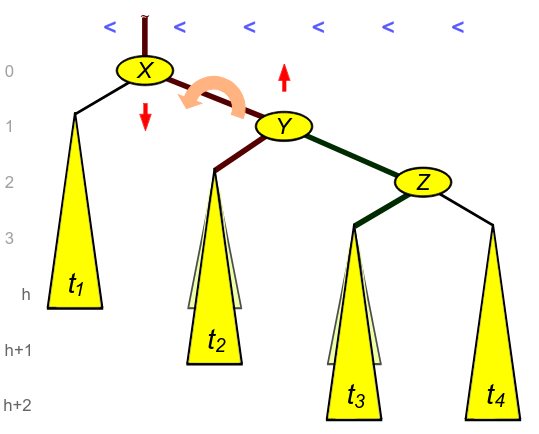
The first step is to perfrom a right rotation so that \(Z\) is a right child of \(Y\). This is shown in the figure below. The subtrees themselves are all about the same height, so performing one more rotation will line up the tree correctly.
Figure 3: An AVL tree with a right-left violation after the first rotation (Wikipedia).
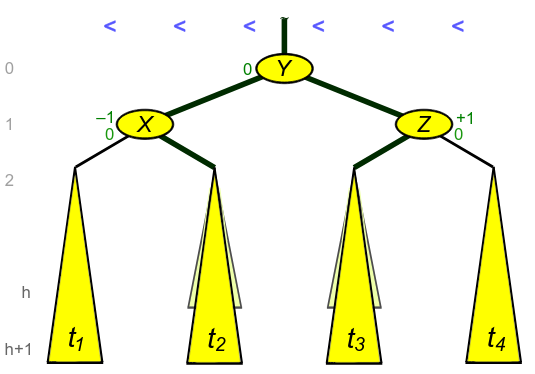
The final step is to perform a left rotation to correct the violation. The tree is now balanced.
Figure 4: An AVL tree with a right-left violation after the second rotation (Wikipedia).