Bipartite Matching
Bipartite Graphs
A bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets \(U\) and \(V\) such that every edge connects a vertex in \(U\) to one in \(V\). There are no edges between vertices within the same set. The matching problem is one you are likely familiar with: given a set of words and a set of definitions, can you pair each word with its correct definition? When it comes to graphs, the matching problem involves finding a set of edges such that no two edges share a common vertex.
Formally, given an undirected graph \(G = (V, E)\), a matching \(M\) is a subset of edges \(M \subseteq E\) such that no two edges in \(M\) share a common vertex. A matching is said to be maximum if it contains the largest possible number of edges.
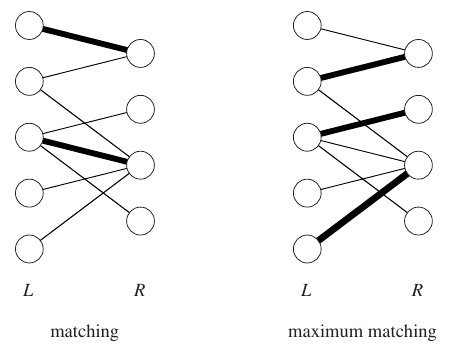
Figure 1: A matching between (L) and (R) in a bipartite graph (left) and a maximum matching (right) (Cormen et al. 2022).
Finding Matchings
A bipartite graph may have many possible candidate edges between nodes. The algorithms discussed herein take an incremental approach that build up a matching one edge at a time. The two primary algorithms for finding maximum matchings in bipartite graphs are the Hopcroft-Karp algorithm and the Hungarian algorithm.
These algorithms rely on the concept of alternating and augmenting paths. An alternating path is a path that alternates between edges that are in the matching and edges that are not. An augmenting path is an alternating path that starts and ends with unmatched vertices.
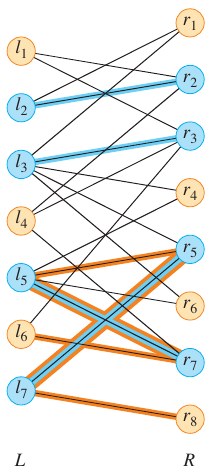
In the figure below, the alternating path is \(\{(l_5, r_5), (l_5, r_7), (l_6, r_7), (l_7, r_5), (l_7, r_8)\}\). The first and last edges are not in the matching, making this an augmenting path.
Figure 2: An augmenting path (highlighted in orange).
Looking at this figure more closely, you can observe that there are 3 edges in the unmatched set compared to 2 in the matched set. By swapping the matched and unmatched edges along this path, we can increase the size of the matching by 1. This process is known as augmenting the matching. However, you might think this an exception rather than the rule. We can formalize this observation, but we first need a helpful definition.
A symmetric difference of two sets \(A\) and \(B\), denoted by \(A \oplus B\), is the set of elements that are in either of the sets but not in their intersection. In other words, it contains elements that are in \(A\) or \(B\) but not in both.