Positional Encoding
What are positional encodings?
Positional encodings are a way to encode the position of elements in a sequence. They are used in the context of sequence-to-sequence models, such as transformers, to provide the model with information about the order of elements in the input sequence. These were not needed for models like RNNs and LSTMs since the order of elements in the input sequence is preserved by the recurrent connections.
Why are positional encodings needed?
Imagine your favorite movie. It is highly likely that the characters evolve over time through their experiences with each other and the environment around them. Your perception of your favorite character is almost certainly influenced by these events. If there was no story, no context, then your summary of them would probably not change from one moment to the next. This is what it would be like for a transformer model with no positional encodings. The representation of each input element would be the same regardless of its position in the sequence, even if the context of the surrounding elements is different.
Properties of Positional Encodings
Positional encodings have been used before in the context of convolutional sequence-to-sequence models (Gehring et al. 2017). I am focusing on three primary properties, but interested readers should check out this great article by Christopher Fleetwood.
Encodings should be unique
The value given for each position should be unique so that input values can be distinguished. It should also be consistent across different sequences lengths. That is, the encoding for the first element in a sequence of length 10 should be the same as the encoding for the first element in a sequence of length 100.
Linearity of position
The positional encoding should be linear with respect to the position of the element in the sequence. This means that the encoding for the first element should be the same distance from the encoding for the second element as the encoding for the second element is from the encoding for the third element.
Generalization to out of training sequence lengths
The positional encoding should generalize to sequences of different lengths than those seen during training. This is important because the model should be able to handle sequences of different lengths during inference.
Sinusoidal Positional Encoding
The positional encoding used in the original Transformer architecture is called sinusoidal positional encoding (Vaswani et al. 2017). Given the position \(pos\) and dimension \(i\) of the input, the encoding is given by
\begin{align*} PE_{pos, 2i} &= \sin\left(\frac{pos}{10000^{2i/d_{model}}}\right)\\ PE_{pos, 2i+1} &= \cos\left(\frac{pos}{10000^{2i/d_{model}}}\right) \end{align*}
Why do we use \(\sin\) and \(\cos\) here? To understand this, we need to return to trigonometry. I also like to go through the following derivation when discussing geometric linear transformations in my linear algebra class. The second property stated above was that the positions between two elements should be linear. For this, let’s ignore the frequency term and only consider the position term.
\begin{align*} PE_{pos} &= \sin(p)\\ PE_{pos+1} &= \cos(p)\\ \end{align*}
Adding some offset of \(k\) to the position \(p\) gives
\begin{align*} PE_{pos+k} &= \sin(p+k)\\ PE_{pos+1+k} &= \cos(p+k)\\ \end{align*}
Using the trigonometric identity \(\sin(a+b) = \sin(a)\cos(b) + \cos(a)\sin(b)\), we can rewrite the above as
\begin{align*} PE_{pos+k} &= \sin(p)\cos(k) + \cos(p)\sin(k)\\ PE_{pos+1+k} &= \cos(p)\cos(k) - \sin(p)\sin(k)\\ \end{align*}
A transformation that can be represented as a matrix multiplication is a linear transformation. So we are looking for a matrix \(M\) such that
\begin{align*} \begin{bmatrix} m_{11} & m_{12}\\ m_{21} & m_{22} \end{bmatrix} \begin{bmatrix} \sin(p)\\ \cos(p) \end{bmatrix} &= \begin{bmatrix} \sin(p)\cos(k) + \cos(p)\sin(k)\\ \cos(p)\cos(k) - \sin(p)\sin(k) \end{bmatrix} \end{align*}
If you know how to multiply matrices, you can see that the matrix
\begin{align*} \begin{bmatrix} \cos(k) & \sin(k)\\ -\sin(k) & \cos(k) \end{bmatrix} \end{align*}
does the trick. This is a rotation matrix, and it is a linear transformation.
Translation and Rotation
An embedded token is special. The combination of values across the embedding dimensions define what the token represents semantically. If we add to those values, we are fundamentally changing the semantic meaning of the token. The sinusoidal positional encoding does exactly that.
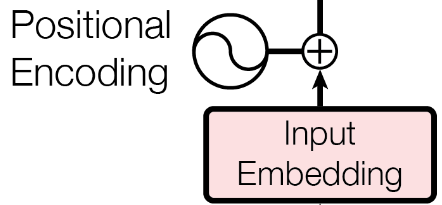
Figure 1: Positional encoding is added to the embedding (Vaswani et al. 2017).
As an alternative, we could rotate the query and key vectors in the self-attention mechanism. This would preserve the magnitude of the token’s representation while only changing the relative angle between them. This is the approach taken by the Rotary Position Embedding (Su et al. 2023).
Rotary Position Embedding (RoPE)
RoPE proposes that the relative positional information be encoded in the product of the query and key vectors of the self-attention mechanism. This is expressed by equation (11) in the original paper (Su et al. 2023).
\[ \langle f_q(\mathbf{x}_m, m), f_k(\mathbf{x}_n, n)\rangle = g(\mathbf{x}_m, \mathbf{x}_n, m - n) \]
The derivation of their solution is a bit involved, but key idea is to rotate the transformed embeddings by an angle that is a multiple of the position index:
\begin{equation*} f_{\{q, k\}}(\mathbf{x}_m, m) = \begin{bmatrix} \cos(m\theta) & -\sin(m\theta)\\ \sin(m\theta) & \cos(m\theta) \end{bmatrix} \begin{bmatrix} W_{\{q, k\}}^{(11)} & W_{\{q, k\}}^{(12)}\\ W_{\{q, k\}}^{(21)} & W_{\{q, k\}}^{(22)} \end{bmatrix} \begin{bmatrix} \mathbf{x}_m^{(1)}\\ \mathbf{x}_m^{(2)} \end{bmatrix} \end{equation*}