Recursion Tree Method
Visualizing the characteristics of an algorithm is a great way to build intuition about its runtime. Although it can be used to prove a recurrence, it is often a good jumping off point for the Substitution Method.
Example 4.13 from CLRS
Consider the recurrence \(T(n) = 3T(n/4) + \Theta(n^2)\). We start by describing \(\Theta(n^2) = cn^2\), where the constant \(c > 0\) serves as an upper-bound constant. It reflects the amount of work done at each level of the recursion tree. The tree is shown below.
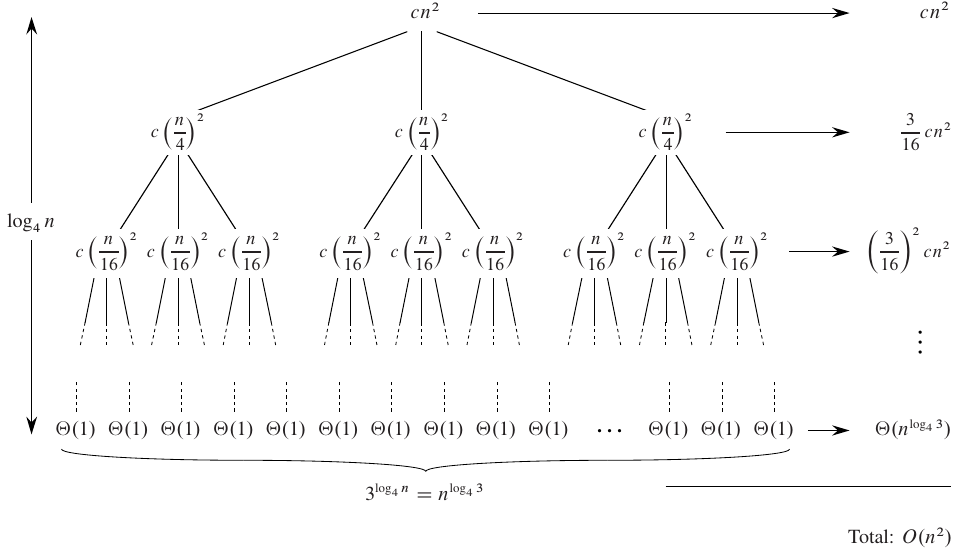
Figure 1: Example 4.13 from CLRS (Cormen et al. 2022)
As the tree expands out over a few levels, we can see a pattern in the cost at depth \(i\). Each level of increasing depth has 3 times as many nodes as the previous. With the exception of the leaves, the cost for each level is \((\frac{3}{16})^i cn^2\). The total cost of the leaves is based on the number of leaves, which is \(3^{\log_4 n}\) since each level has \(3^i\) nodes and the depth is \(\log_4 n\). Using the identity \(a^{\log_b c} = c^{\log_b a}\), we can simplify the leaves to \(n^{\log_4 3}\). The total cost of the leaves is \(\Theta(n^{\log_4 3})\).
The last step is to add up the costs over all levels:
\begin{align*} T(n) &= \sum_{i=0}^{\log_4 n} \left( \frac{3}{16} \right)^i cn^2 + \Theta(n^{\log_4 3}) \\ &< \sum_{i=0}^{\infty} \left( \frac{3}{16} \right)^i cn^2 + \Theta(n^{\log_4 3}) \\ &= \frac{cn^2}{1 - \frac{3}{16}} + \Theta(n^{\log_4 3}) \\ &= \frac{16}{13}cn^2 + \Theta(n^{\log_4 3}) \\ &= \Theta(n^2). \end{align*}
The second line in the equation is a geometric series.
Verifying using the Substitution Method
Even if we weren’t so particular with the maths, the recursion tree method is a great way to build intuition about the runtime. Let’s verify that this recurrence is bounded above by \(O(n^2)\) using the Substitution Method.
Here we show that \(T(n) \leq dn^2\) for a constant \(d > 0\). The previous constant \(c > 0\) is reused to describe the cost at each level of the recursion tree.
\begin{align*} T(n) &\leq 3T(n/4) + cn^2 \\ &\leq 3(d(n/4)^2) + cn^2 \\ &= \frac{3}{16}dn^2 + cn^2 \\ &\leq dn^2 \text{ if } d \geq \frac{16}{13}c. \end{align*}
Exercises
- Solve the recurrence \(T(n) = 2T(n/2) + cn\) using the recursion tree method.