Red-Black Trees are modified Binary Search Trees that maintain a balanced structure in order to guarantee that operations like search, insert, and delete run in \(O(\log n)\) time.
Definition
A red-black tree is a binary search tree with the following properties:
- Every node is either red or black.
- The root is black.
- Every
NULLleaf is black. - If a node is red, then both its children are black.
- For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.
Figure 1: Red-Black Tree from CLRS Chapter 13.
The only structural addition we need to make over a BST is the addition of a color attribute to each node. This attribute can be either RED or BLACK.
Property 5 implies that the black-height of a tree is an important property. This property is used to prove that the height of a red-black tree with \(n\) internal nodes is at most \(2 \log(n + 1)\).
Operations
Rotate
If a binary search tree is balanced, then searching for a node takes \(O(\log n)\) time. However, if the tree is unbalanced, then searching can take \(O(n)\) time. When items are inserted or deleted from a tree, it can become unbalanced. Without any way to correct for this, a BST is less desirable unless the data will not change.
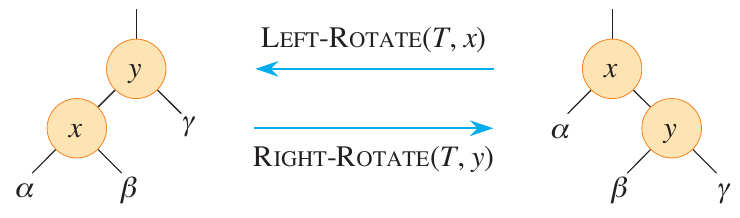
When nodes are inserted or deleted into a red-black tree, the rotation operation is used in functions that maintain the red-black properties. This ensures that the tree remains balanced and that operations like search, insert, and delete run in \(O(\log n)\) time. The figure below shows the two types of rotations that can be performed on a red-black tree.
Figure 2: Rotations in a red-black tree (CLRS Figure 13.2).
Python implementations of both left and right rotations are given below.
def left_rotate(self, x):
y = x.right
x.right = y.left
if y.left != self.nil:
y.left.p = x
y.p = x.p
if x.p == self.nil:
self.root = y
elif x == x.p.left:
x.p.left = y
else:
x.p.right = y
y.left = x
x.p = y
def right_rotate(self, y):
x = y.left
y.left = x.right
if x.right != self.nil:
x.right.p = y
x.p = y.p
if y.p == self.nil:
self.root = x
elif y == y.p.left:
y.p.left = x
else:
y.p.right = x
x.right = y
y.p = x
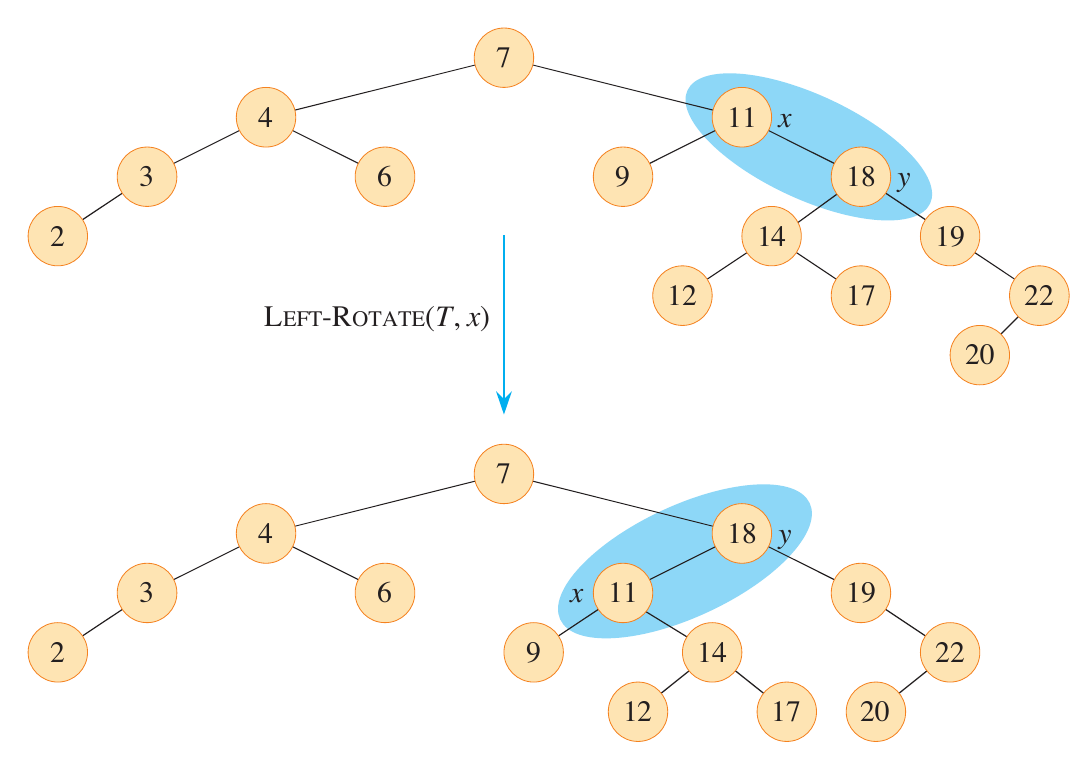
Cormen et al. Figure 13.3 (below) shows the result of performing a left rotation on node \(x\).
Figure 3: Left rotation on node (x) (CLRS Figure 13.3).
A rotation only changes pointer assignments, so it takes \(O(1)\) time.
Insert
The insert operation in a red-black tree starts off identically to the insert operation in a BST. The new node is inserted into the tree as a leaf node. Since the NULL leaf nodes must be black by definition, the added node is colored red. The function in Python is shown below.
def insert(self, z):
y = self.nil
x = self.root
while x != self.nil:
y = x
if z.key < x.key:
x = x.left
else:
x = x.right
z.p = y
if y == self.nil:
self.root = z
elif z.key < y.key:
y.left = z
else:
y.right = z
z.left = self.nil
z.right = self.nil
z.color = RED
self.insert_fixup(z)
By adding the node and setting its color to red, we have possibly violated properties 2 and 4. Property 2 is violated if z is the root. Property 4 is violated if the parent of the new node is also red. The final line of the function calls insert_fixup to restore the red-black properties. It is defined as follows.
def insert_fixup(self, z):
while z.p.color == RED:
if z.p == z.p.p.left:
y = z.p.p.right
if y.color == RED:
z.p.color = BLACK
y.color = BLACK
z.p.p.color = RED
z = z.p.p
else:
if z == z.p.right:
z = z.p
self.left_rotate(z)
z.p.color = BLACK
z.p.p.color = RED
self.right_rotate(z.p.p)
else:
y = z.p.p.left
if y.color == RED:
z.p.color = BLACK
y.color = BLACK
z.p.p.color = RED
z = z.p.p
else:
if z == z.p.left:
z = z.p
self.right_rotate(z)
z.p.color = BLACK
z.p.p.color = RED
self.left_rotate(z.p.p)
self.root.color = BLACK
The main logic of this is that the loop will continue to make corrections up the tree until it reaches the root, which must be a black node.
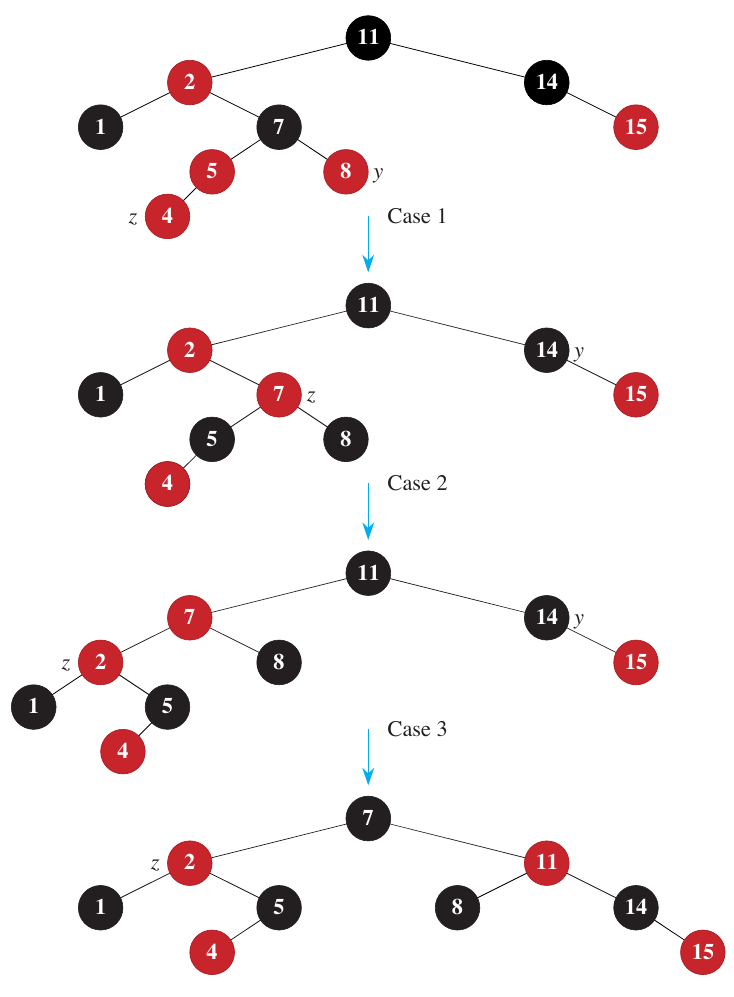
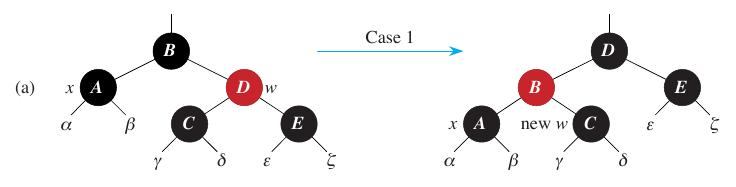
Case 1
Inside the while loop, the first and second conditions are symmetric. One considers the case where z’s parent is a left child, and the other considers the case where z’s parent is a right child. Further, if z’s parent is a left child, then we start by setting y to z’s aunt. Let’s investigate the first if statement, where y is RED. In this case, both z’s parent and aunt are RED. We can fix this by setting both to BLACK and setting z’s grandparent to RED. This may violate property 2, so we set z to its grandparent and repeat the loop.
if y.color == RED:
z.p.color = BLACK
y.color = BLACK
z.p.p.color = RED
z = z.p.p
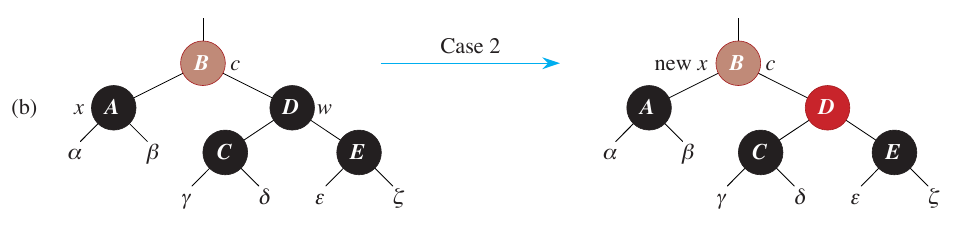
Case 2
If y is BLACK, then we need to consider the case where z is a right child. In this case, we set z to its parent and perform a left rotation. This automatically results in the third case, where z is a left child.
if z == z.p.right:
z = z.p
self.left_rotate(z)
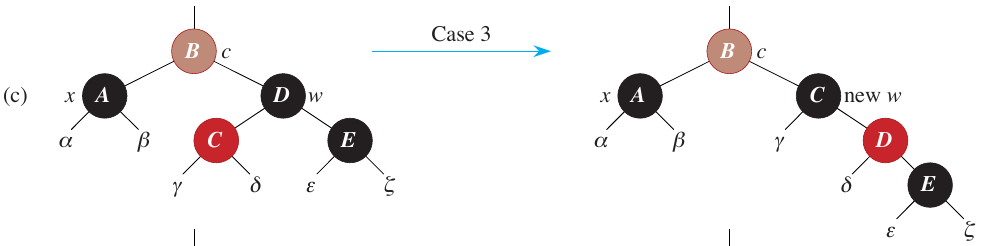
Case 3
If z is a left child, then we set z’s parent to BLACK and its grandparent to RED. Then we perform a right rotation on the grandparent.
z.p.color = BLACK
z.p.p.color = RED
self.right_rotate(z.p.p)
Figure 13.4 from Cormen et al. demonstrates the addition of a node to a red-black tree. The node is inserted as a leaf node and colored red. Then insert_fixup is called to restore the red-black properties.
Figure 4: Inserting a node into a red-black tree (CLRS Figure 13.4).
The insert operation takes \(O(\log n)\) time since it performs a constant number of rotations.
Delete
Like the delete operation of a BST, the delete operation of a RBT uses a transplant operation to replace the deleted node with its child. The transplant operation is defined as follows.
def transplant(self, u, v):
if u.p == self.nil:
self.root = v
elif u == u.p.left:
u.p.left = v
else:
u.p.right = v
v.p = u.p
The full delete operation follows a similar structure to that of its BST counterpart. There are a few distinct differences based on the color of the node being deleted. The function begins as follows.
def delete(self, z):
y = z
y_original_color = y.color
The first line sets y to the node to be deleted. The second line saves the color of y. This is necessary because y will be replaced by another node, and we need to know the color of the replacement node. The first two conditionals check if z has any children. If there is right child, then the z is replaced by the left child. If there is a left child, then z is replaced by the right child. If z has no children, then z is replaced by NULL.
if z.left == None:
x = z.right
self.transplant(z, z.right)
elif z.right == None:
x = z.left
self.transplant(z, z.left)
If z has two children, then we find the successor of z and set y to it. The successor is the node with the smallest key in the right subtree of z. The successor is guaranteed to have at most one child, so we can use the code above to replace y with its child. Then we replace z with y.
else:
y = self.minimum(z.right)
y_original_color = y.color
x = y.right
if y != z.right: # y is farther down the tree
self.transplant(y, y.right)
y.right = z.right
y.right.p = y
else:
x.p = y
self.transplant(z, y)
y.left = z.left
y.left.p = y
y.color = z.color
The procedure kept track of y_original_color to see if any violations occurred. This would happen if y was originally BLACK because the transplant operation, or the deletion itself, could have violated the red-black properties. If y_original_color is BLACK, then we call delete_fixup to restore the properties.
Delete Fixup
If the node being deleted is BLACK, then the following scenarios can occur. If y is the root and a RED child of y becomes the new root, property 2 is violated. Let x be a RED child of y, if a new parent of x is RED, then property 4 is violated. Lastly, removing y may have caused a violation of property 5, since any path containing y has 1 less BLACK node in it.
Correcting violation 5 can be done by transferring the BLACK property from y to x, the node that moves into y’s original position. This requires us to allow nodes to take on multiple counts of colors. That is, if x was already BLACK, it becomes double BLACK. If it was RED, it becomes RED-AND-BLACK. There is a good reason to this extension, as it will help us decide which case of delete_fixup to use.
The delete_fixup function will restore violations of properties 1, 2, and 4. It is called after the delete operation, and it takes a single argument, x, which is the node that replaced the deleted node. It performs a series of rotations and color changes to restore the violated properties.
Let’s look at the delete_fixup function from the ground up. It is a little more complex than insert_fixup because it has to handle the case where the node being deleted is BLACK. In total, there are 4 distinct cases per side. Like insert_fixup, it is enough to understand the first half, as the second is symmetric. The function begins as follows, where x is a left child.
Case 1
def delete_fixup(self, x):
while x != self.root and x.color == BLACK:
if x == x.p.left:
w = x.p.right
if w.color == RED:
w.color = BLACK
x.p.color = RED
self.left_rotate(x.p)
w = x.p.right
In the first case, x’s sibling w is RED. If this is true, then w must have two BLACK subnodes. The colors of w and x’s parent are then switched, and a left rotation is performed on x’s parent. The result of case 1 converts to one of cases 2, 3, or 4. The figure below shows the result of the first case.
Figure 5: Case 1 of delete_fixup (CLRS Figure 13.7).
Case 2
if w.left.color == BLACK and w.right.color == BLACK:
w.color = RED
x = x.p
If both of w’s subnodes are BLACK and both w and x are also black (actually, x is doubly BLACK), then there is an extra BLACK node on the path from w to the leaves. The colors of both x and w are switched, which leaves x with a single BLACK count and w as RED. The extra BLACK property is transferred to x’s parent. The figure below shows the result of the second case.
Figure 6: Case 2 of delete_fixup (CLRS Figure 13.7).
Case 3
else:
if w.right.color == BLACK:
w.left.color = BLACK
w.color = RED
self.right_rotate(w)
w = x.p.right
If w is BLACK, its left child is RED, and its right child is BLACK, then the colors of w and its left child are switched. Then a right rotation is performed on w. This rotation moves the BLACK node to w’s position, which is now the new sibling of x. This leads directly to case 4. A visualization of case 3 is shown below.
Figure 7: Case 3 of delete_fixup (CLRS Figure 13.7).
Case 4
w.color = x.p.color
x.p.color = BLACK
w.right.color = BLACK
self.left_rotate(x.p)
x = self.root
At this point, w is BLACK and its right child is RED. Also remember that x still holds an extra BLACK count. This last case performs color changes and a left rotation which remedy the extra BLACK count. The figure below shows the result of case 4.
Figure 8: Case 4 of delete_fixup (CLRS Figure 13.7).
The full delete_fixup function is shown below.
def delete_fixup(self, x):
while x != self.root and x.color == BLACK:
if x == x.p.left:
w = x.p.right
if w.color == RED:
w.color = BLACK
x.p.color = RED
self.left_rotate(x.p)
w = x.p.right
if w.left.color == BLACK and w.right.color == BLACK:
w.color = RED
x = x.p
else:
if w.right.color == BLACK:
w.left.color = BLACK
w.color = RED
self.right_rotate(w)
w = x.p.right
w.color = x.p.color
x.p.color = BLACK
w.right.color = BLACK
self.left_rotate(x.p)
x = self.root
else:
w = x.p.left
if w.color == RED:
w.color = BLACK
x.p.color = RED
self.right_rotate(x.p)
w = x.p.left
if w.right.color == BLACK and w.left.color == BLACK:
w.color = RED
x = x.p
else:
if w.left.color == BLACK:
w.right.color = BLACK
w.color = RED
self.left_rotate(w)
w = x.p.left
w.color = x.p.color
x.p.color = BLACK
w.left.color = BLACK
self.right_rotate(x.p)
x = self.root
x.color = BLACK
The delete operation takes \(O(\log n)\) time since it performs a constant number of rotations. The delete_fixup operation also takes \(O(\log n)\) time since it performs a constant number of color changes and at most 3 rotations. Case 2 of delete_fixup could move the violation up the tree, but this would happen no more than \(O(\log n)\) times. In total, the delete operation takes \(O(\log n)\) time.
Exercises
- Create a red-black tree class in Python that supports the operations discussed in these notes.
- Using the created class from exercise 1, implement a Hash Map class that uses a red-black tree for collision resolution via chaining.