Sparse Matrix Computation
Introduction
Sparse matrices are matrices with mostly zero elements. They are common in scientific computing, machine learning, and other fields. It is important to study them in the context of GPU computing because they can be very large and require a lot of memory. Effeciently representing and computing with sparse matrices provides a substantial benefit to many applications.
The obvious benefits of sparsity is that we can typically represent the same matrix using a smaller memory footprint. Fewer elements means fewer wasted operations as well. The challenges of GPU implementations are that the memory access patterns are not always friendly to the GPU architecture. This is especially true for sparse matrices, where the memory access patterns are often irregular.
These notes will review the sparse matrix formats as presented in (Hwu, Kirk, and El Hajj 2022). Each will be evaluated using the following criteria:
- Compaction: How well does the format compact the data?
- Flexibility: Is the format easy to modify?
- Accessibility: How easy is it to access the data?
- Memory access efficiency: Are the accesses coalesced?
- Load balance: Are the operations balanced across threads?
Coordinate List Format (COO)
This format stores non-zero elements in a 1D array of values. It also requires two 1D arrays to store the row and column indices, incurrent an overhead of 2N. The values in each array are contiguous, which is good for memory access.
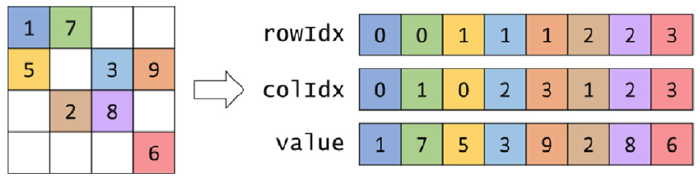
Figure 1: COO Format (Hwu, Kirk, and El Hajj 2022).
Kernel Implementation
__global__ void spmv_coo_kernel(COOMatrix cooMatrix, float *x, float *y) {
int i = blockIdx.x * blockDim.x + threadIdx.x;
if (i < cooMatrix.numNonzeros) {
int row = cooMatrix.rowIdx[i];
int col = cooMatrix.colIdx[i];
float val = cooMatrix.values[i];
atomicAdd(&y[row], val * x[col]);
}
}
Evaluation
- Compaction: Compared to representing the matrices in dense format, the COO format is very compact. However, it is not as compact as some other sparse matrix formats. It requires an additional over head of 2N elements to store the row and column indices.
- Flexibility: Indices and values can be easily modified in this format. This is good for applications that require frequent modifications.
- Accessibility: It is easy to access nonzero elements. It is not easy to access the original 0s in each row.
- Memory access efficiency: The values in this format are contiguous, resulting in coalesced memory access.
- Load balance: The data is uniformly distributed across threads, resulting in good load balance.
One major drawback, as seen in the code above, is the use of atomic operations.
Compressed Sparse Row Format (CSR)
The key idea of this format is that each thread is responsible for all nonzeros in a row.
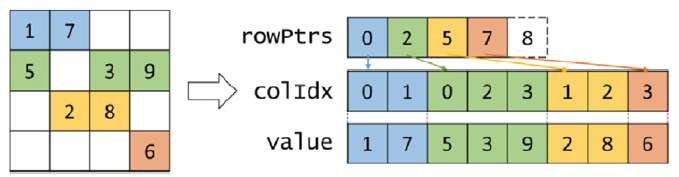
Figure 2: CSR Format (Hwu, Kirk, and El Hajj 2022).
Kernel Implementation
__global__ void spmv_csr_kernel(CSRMatrix csrMatrix, float *x, float *y) {
int row = blockIdx.x * blockDim.x + threadIdx.x;
if (row < csrMatrix.numRows) {
float sum = 0.0f;
for (int j = csrMatrix.rowPtr[row]; j < csrMatrix.rowPtr[row + 1]; j++) {
sum += csrMatrix.values[j] * x[csrMatrix.colIdx[j]];
}
y[i] = sum;
}
}
The rows are mapped to a single pointer index, so it only needs \(m\) entries to store them. The columns are not required to be in order. If the columns are in order, the data is represented in row-major order without the zero elements.
Evaluation
- Compaction: The CSR format is more compact than the COO format since it only requires \(m\) entries to store the row pointers.
- Flexibility: The CSR format is not as flexible as the COO format. It is not easy to modify the values or indices.
- Accessibility: There is less parallelization than COO due to the row sizes.
- Memory access efficiency: The memory access pattern is poor since the data is separated over columns.
- Load balance: The load is not balanced across threads. Some threads will have more work than others, leading to control divergence.
ELL Format
ELL fixes the non-coalesced memory accesses of CSR via data padding and transposition. This is visualized below:
- Start with CSR format
- Pad rows to equal size
- Store in column-major order
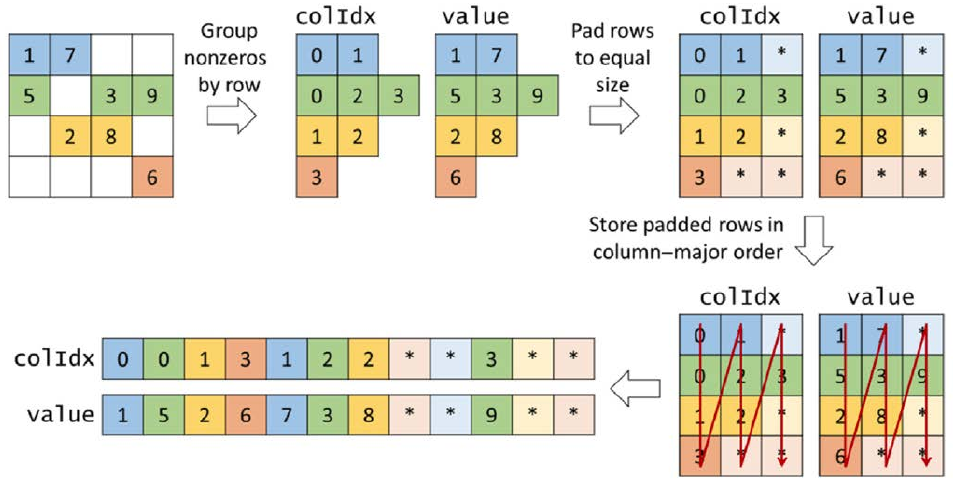
Figure 3: ELL Format (Hwu, Kirk, and El Hajj 2022).
Kernel Implementation
__global__ void spmv_ell_kernel(ELLMatrix ellMatrix, float *x, float *y) {
int row = blockIdx.x * blockDim.x + threadIdx.x;
if (row < ellMatrix.numRows) {
float sum = 0.0f;
for (int j = 0; j < ellMatrix.nnzPerRow[row]; j++) {
int col = ellMatrix.colIdx[j * ellMatrix.numRows + row];
sum += ellMatrix.values[j * ellMatrix.numRows + row] * x[col];
}
y[row] = sum;
}
}
Evaluation
- Compaction: Padding the rows means this is less space efficient than CSR.
- Flexibility: More flexible than CSR; adding nonzeros in CSR requires a shift of values. This format can replaced a padded element if necessary.
- Accessibility: ELL can return the row given the index of a nonzero element as well as the nonzero of a row given that index.
- Memory access efficiency: Consecutive threads access consecutive memory locations.
- Load balance: Shares the same control divergence issues as CSR.
ELL-COO Format
ELL-COO combines the two formats to improve space efficiency and control divergence.
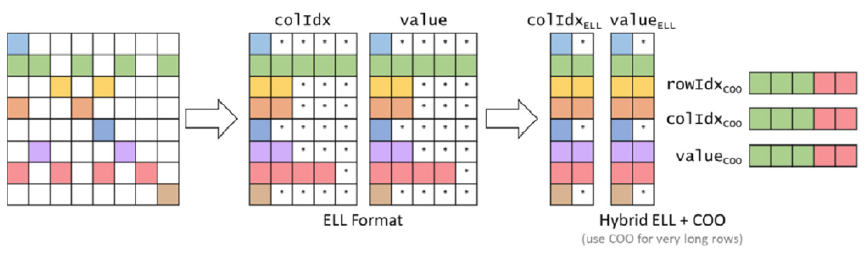
Figure 4: ELL-COO Format (Hwu, Kirk, and El Hajj 2022).
Evaluation
- Compaction: ELL-COO has the same compaction as ELL.
- Flexibility: ELL-COO is more flexible than ELL thanks to inclusion of the COO format.
- Accessibility: It is not always possible to access all nonzeros given a row index.
- Memory access efficiency: The memory access pattern is coalesced.
- Load balance: COO reduces the control divergence seen in ELL alone.
Jagged Diagonal Storage Format (JDS)
The last format we will consider is the Jagged Diagonal Storage format. This format reduces divergence and improves memory coalescing without padding. The main idea is to sort the rows by length from longest to shortest.
- Group nonzeros by row
- Sort rows by length while preserving their original row indices
- Store in column-major order
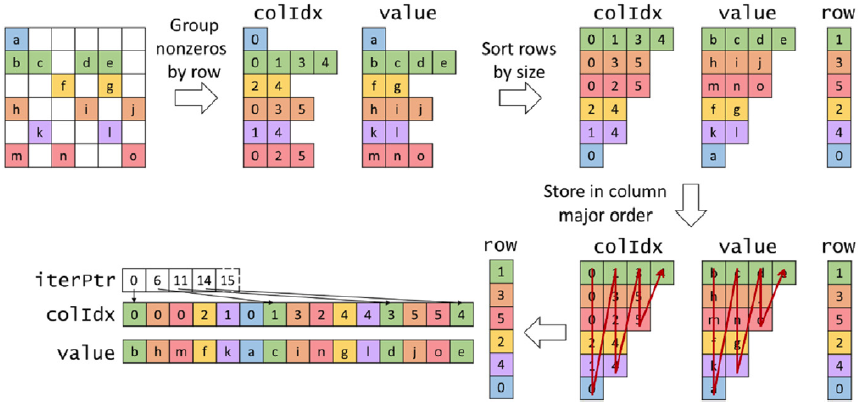
Figure 5: JDS Format (Hwu, Kirk, and El Hajj 2022).
Evaluation
- Compaction: Avoid paddding, so it is more space efficient than ELL.
- Flexibility: Less flexible than ELL since it requires sorting when adding new elements.
- Accessibility: Cannot access a row and column given the index of a nonzero element.
- Memory access efficiency: Without padding, the starting location of memory accesses in each iteration can vary.
- Load balance: Since the rows are sorted, threads of the same warp are likely to iterate over rows of similar length.