Transformers

Nov 6, 2022 6 min read

Table of Contents

Introduction
Definition
Attention
Key-value Store
Scaled Dot Product Attention
Multi-Head Attention
Encoder-Decoder Architecture
Encoder
Decoder
Usage
Resources

Introduction

The story of Transformers begins with “Attention Is All You Need” (Vaswani et al., n.d.). In this seminal work, the authors describe the current landscape of sequential models, their shortcomings, and the novel ideas that result in their successful application.

Their first point highlights a fundamental flaw in how Recurrent Neural Networks process sequential data: their output is a function of the previous time step. Given the hindsight of 2022, where large language models are crossing the trillion parameter milestone, a model requiring recurrent computation dependent on previous time steps without the possibility of parallelization would be virtually intractable.

The second observation refers to attention mechanisms, a useful addition to sequential models that enable long-range dependencies focused on specific contextual information. When added to translation models, attention allows the model to focus on particular words (Bahdanau, Cho, and Bengio 2016).

The Transformer architecture considers the entire sequence using only attention mechanisms. There are no recurrence computations in the model, allowing for higher efficiency through parallelization.

Definition

The original architecture consists of an encoder and decoder, each containing one or more attention mechanisms. Not every type of model uses both encoders and decoders. This is discussed later [TODO: discuss model types]. Before diving into the architecture itself, it is important to understand what an attention mechanism is and how it functions.

Attention

Attention mechanisms produce relationships between sequences. When we look at an image of a dog running in a field with the intent of figuring out what the dog is doing in the picture, we pay greater attention to the dog and look at contextual cues in the image that might inform us of their task. This is an automatic process which allows us to efficiently process information.

Attention mechanisms follow the same concept. Consider a machine translation task in which a sentence in English is translated to French. Certain words between the input and output will have stronger correlations than others.

Soft Attention

Use of context vector that is dependent on a sequence of annotations. These contain information about the input sequence with a focus on the parts surrounding the $i$-th word.

\[ c_i = \sum_{j=1}^{T_x}\alpha_{ij}h_j \]

What is $\alpha_{ij}$ and how is it computed? This comes from an alignment model which assigns a score reflecting how well the inputs around position $j$ and output at position $i$ match, given by

\[ e_{ij} = a(s_{i-1}, h_j), \]

where $a$ is a feed-forward neural network and $h_j$ is an annotation produced by the hidden layer of a BRNN. These scores are passed to the softmax function so that $\alpha_{ij}$ represents the weight of annotation $h_j$:

\[ \alpha_{ij} = \frac{\exp(e_{ij})}{\sum_{k=1}^{T_x} \exp (e_{ik})}. \]

This weight reflects how important $h_j$ is at deciding the next state $s_i$ and generating $y_i$.

Soft vs. Hard Attention

This mechanism was also described in the context of visual attention as “soft” attention (Xu et al. 2016). The authors also describe an alternative version they call “hard” attention. Instead of providing a probability of where the model should look, hard attention provides a single location that is sampled from a multinoulli distribution parameterized by $\alpha_i$.

\[ p(s_{t,i} = 1 | s_{j<t}, \mathbf{a}) = \alpha_{t,i} \]

Here, $s_{t,i}$ represents the location $i$ at time $t$, $s_{j<t}$ are the location variables prior to $t$, and $\mathbf{a}$ is an image feature vector.

<span class="figure-number">Figure 1: </span>Hard attention for "A man and a woman playing frisbee in a field." (Xu et al.) — Figure 1: Hard attention for “A man and a woman playing frisbee in a field.” (Xu et al.)

<span class="figure-number">Figure 2: </span>Soft attention for "A woman is throwing a frisbee in a park." (Xu et al.) — Figure 2: Soft attention for “A woman is throwing a frisbee in a park.” (Xu et al.)

The two figures above show the difference between soft and hard attention. Hard attention, while faster at inference time, is non-differentiable and requires more complex methods to train (TODO: cite Luong).

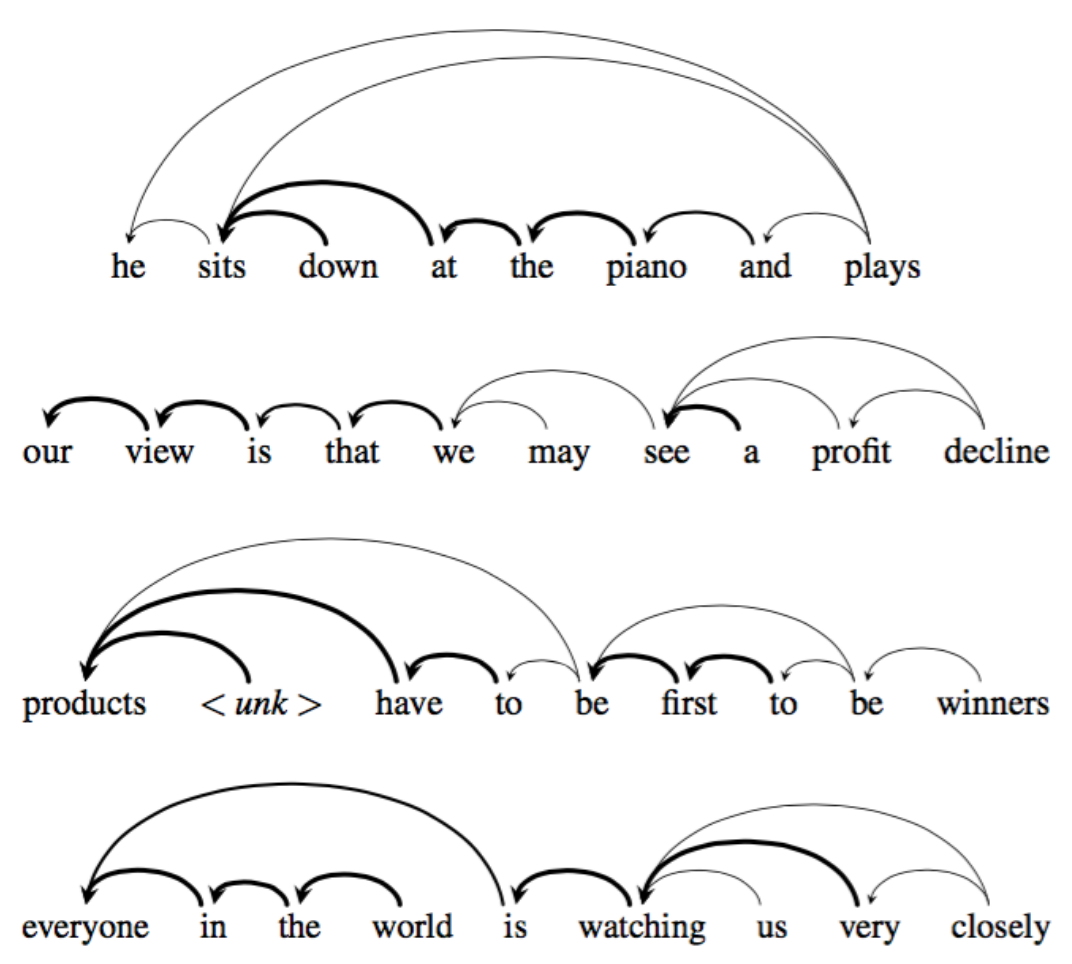
Self-Attention

Self attention is particularly useful for determining the relationship between different parts of an input sequence. The figure below demonstrates self-attention given an input sentence (Cheng, Dong, and Lapata 2016).

How aligned the two vectors are.

Cross Attention

TODO

Key-value Store

Query, key, and value come from the same input (self-attention).

Check query against all possible keys in the dictionary. They have the same size. The value is the result stored there, not necessarily the same size. Each item in the sequence will generate a query, key, and value.

The attention vector is a function of they keys and the query.

Hidden representation is a function of the values and the attention vector.

The Transformer paper talks about queries, keys, and values. This idea comes from retrieval systems. If you are searching for something (a video, book, song, etc.), you present a system your query. That system will compare your query against the keys in its database. If there is a key that matches your query, the value is returned.

\[ att(q, \mathbf{k}, \mathbf{v}) = \sum_i v_i f(q, k_i), \] where $f$ is a similarity function.

This is an interesting and convenient representation of attention. To implement this idea, we need some measure of similarity. Why not orthogonality? Two vectors that are orthogonal produce a scalar value of 0. The maximum value two vectors will produce as a result of the dot product occurs when the two vectors have the exact same direction. This is convenient because the dot product is simple and efficient and we are already performing these calculations in our deep networks in the form of matrix multiplication.

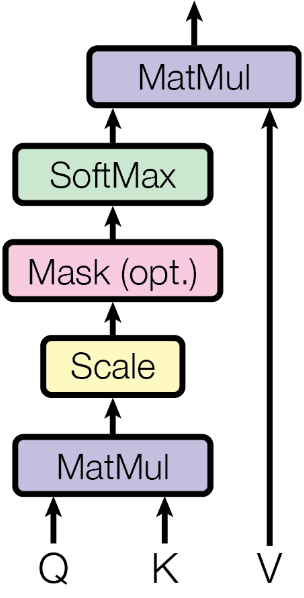
Scaled Dot Product Attention

Each query vector is multiplied with each key using the dot product. This is implemented more efficiently via matrix multiplication. A few other things are added here to control the output. The first is scaling.

Multi-Head Attention

A single attention head can transform the input into a single representation. Is this analagous to using a single convolutional filter? The benefit of having multiple filters is to create multiple possible representations from the same input.

Encoder-Decoder Architecture

The original architecture of a transformer was defined in the context of sequence transduction tasks, where both the input and output are sequences. The most common task of this type is machine translation.

Encoder

The encoder layer takes an input sequence $\{\mathbf{x}_t\}_{t=0}^T$ and transforms it into another sequence $\{\mathbf{z}_t\}_{t=0}^T$.

What is $\mathbf{z}_t$?
How is it used? Input as key and value into second multi-head attention layer of the decoder.
Could you create an encoder only model? Yes. Suitable for classification tasks – classify the representation produced by the encoder. How does this representation relate to understanding?
It’s a transformation to another representation.

Generated representation also considers the context of other parts of the same sequence (bi-directional).

Decoder

Generates an output sequence.
Decoder-only models? Suitable for text generation.
What does the input represent?
What does the output represent?

What if we don’t use an encoder, what information is added in lieu of the encoder output?

Model	Examples	Tasks
Encoder	ALBERT, BERT, DistilBERT, ELECTRA, RoBERTa	Sentence classification, named entity recognition, extractive question answering
Decoder	CTRL, GPT, GPT-2, Transformer XL	Text generation
Encoder-decoder	BART, T5, Marian, mBART	Summarization, translation, generative question answering

Usage